Adaptive Models of Non-Stationary Dynamics in Capital Markets

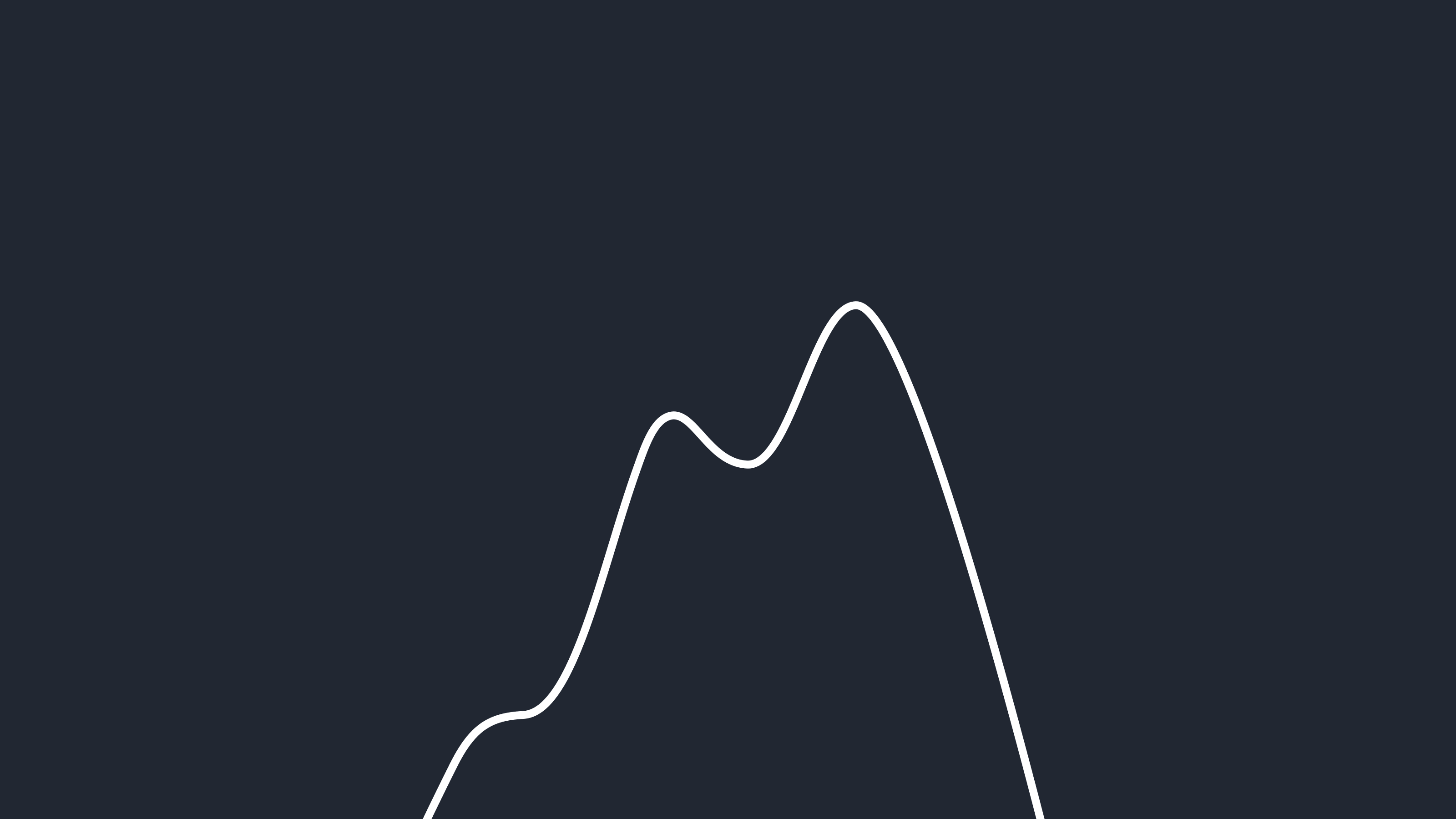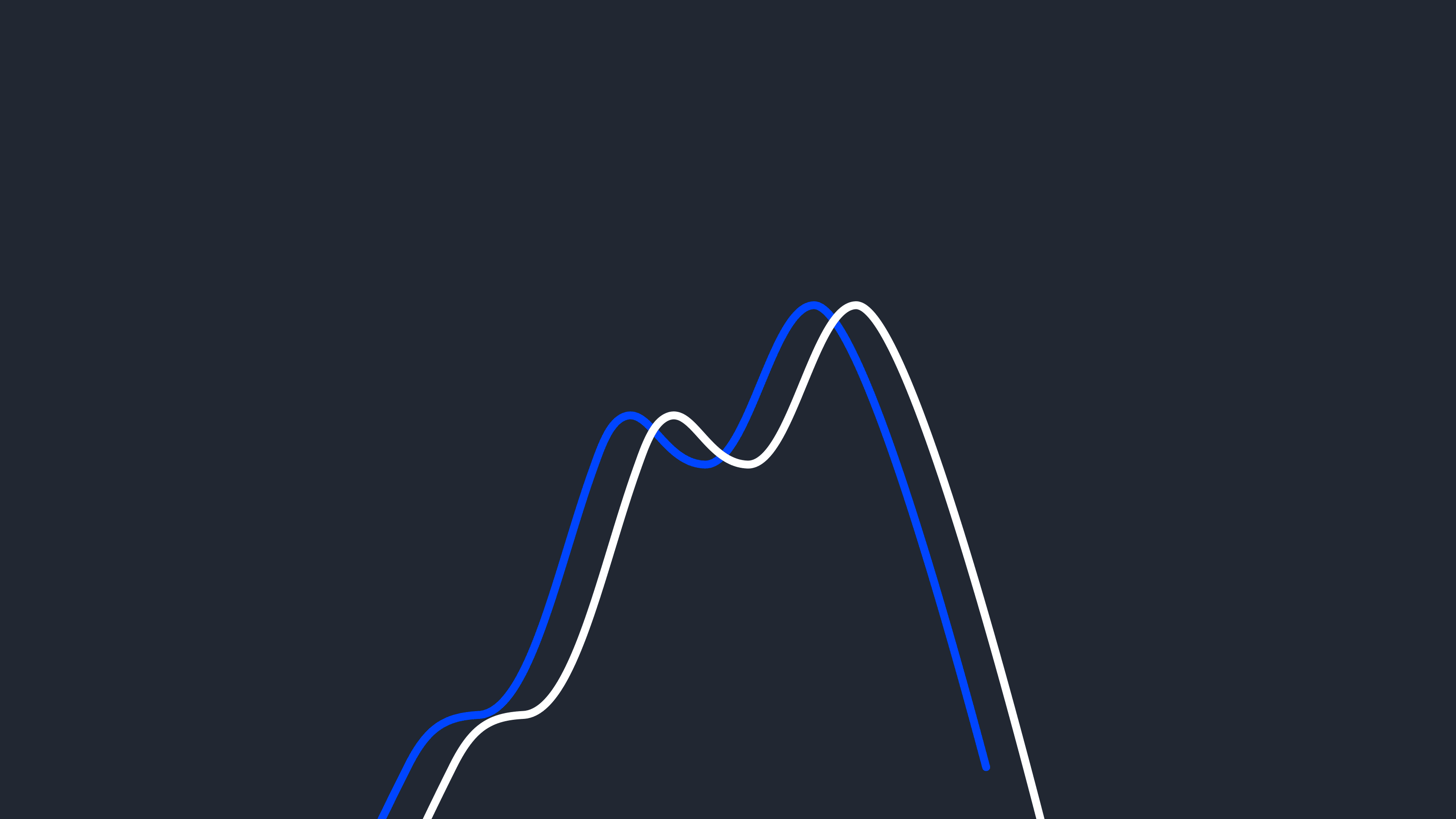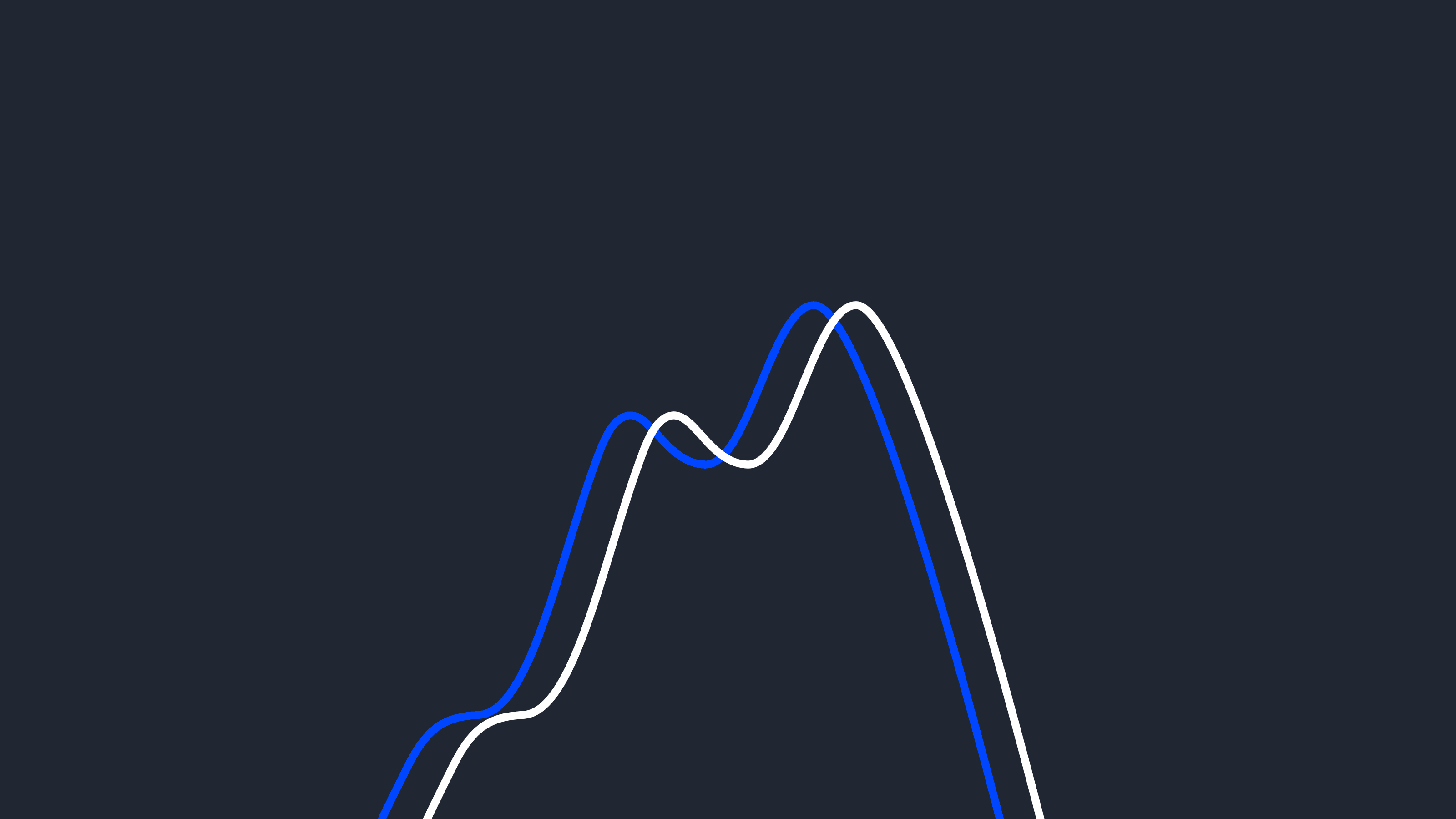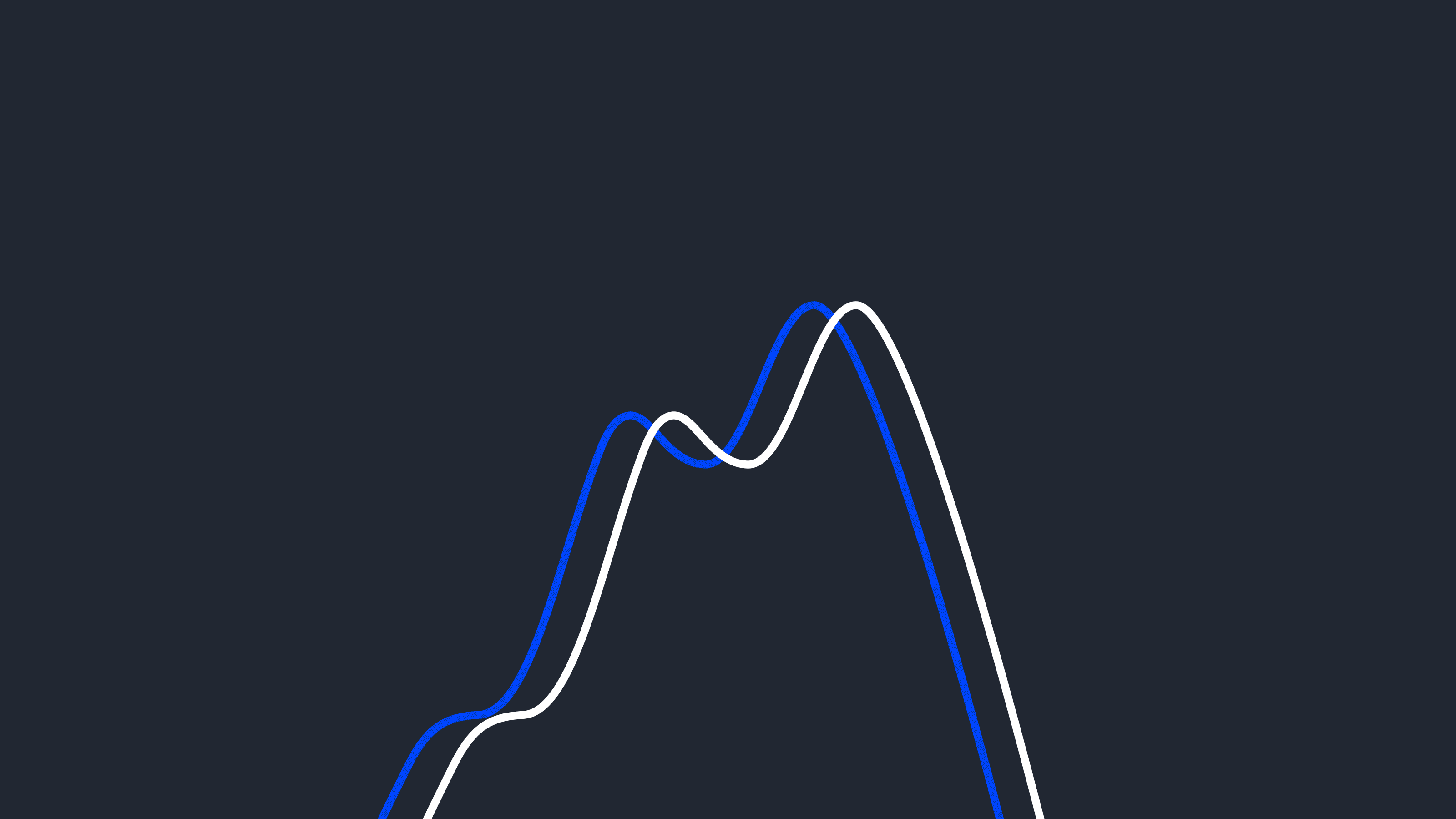
Capital markets are complex and dynamic environments that generate large amounts of time series data at a high frequency. Understanding and modeling the hidden dynamics within capital markets using a data-driven approach is an exciting but challenging task. At its core, time series modeling and forecasting can be expressed as the generation or prediction of ${y}_t \in \mathbb{R}^P$ given previous observations ${y}_{<t} = {\{y}_s \in \mathbb{R}^P: s < t\}$, where ${t}$ and ${s}$ index time. A time series model (for forecasting) is thus essentially a model of the conditional distribution $p({y}_t | {y}_{<t})$. Here we assume discrete time, but the concepts we discuss can be extended to continuous time as well. Figure 1 shows an illustration of (multi-step) time series forecasting, where we predict the next ${H}$ observations given the previous observations from ${t = 1}$ to ${T}$.

However, different from typical time series modeling and forecasting, capital markets involve many participants that act and compete in a shared environment, where the environment as a whole is also heavily influenced by external events, such as news and politics. These complications make the generative process of the time series non-stationary — $p({y}_t|{y}_{<t})$ can undergo a substantial stochastic change over time. This causes significant challenges not only for learning a consistent model from the data but also for applying any learned model at test time effectively and securely.

Stationarity, Non-Stationarity, and Their Nuances

Non-stationarity generally means that the distribution of the data generative process can change over time. It is a problem we may face in time series modeling not only in capital markets but also in other real-world applications. Existing definitions of different types of stationarity (and non-stationarity) include, e.g., strong stationarity and weak stationarity, but we argue that there are important nuances in defining (non-)stationarity in a way that is relevant and useful for time series modeling and forecasting.

We are interested in modeling $p({y})$, where ${y}$ is the target time series, and typically also assume that the distribution of ${y}_t$ can depend on an input variable (feature) ${x}_t \in \mathbb{R}^Q$ that we observe at each time step ${t}$. A com- mon assumption when modeling the resulting conditional distribution $p({y} | {x})$ for the purpose of forecasting is that, given ${x}_t$, ${y}_t$ does not depend on other ${x}_{s}$, ${s} \neq {t}$, such that $p({y} | {x})$ factorizes as follows:

\begin{equation}
p({y} | {x}) = \prod_{t=1}^T p({y}_t | {y}_{< t}, {x}_{t}).
\tag1
\end{equation}

Based on the above equation, we can categorize non-stationarity of y into the following cases:
1. Neither $p({y}_t | {y}_{< t}, {x}_{t})$ nor $p({x}_t)$ changes, but ${y}$ is still not stationary (joint non-stationarity).

2. $p({x}_t)$ changes (covariate non-stationarity).

3. $p({y}_t | {y}_{< t}, {x}_t)$ changes (conditional non-stationarity).

4. A combination of 2 and 3, where both the covariate distribution $p({x}_t)$ and the conditional distribution $p({y}_t | {y}_{< t}, {x}_{t})$ change.

When we say $p({y}_t | {y}_{< t}, {x}_{t})$ does not change, we assume the following:

Assumption 1 ${y}_t$ only depends on a bounded history of ${y}$ for all ${t}$. That is, there exists ${B \in \mathbb{Z}, 0 \le B <\infty}$, such that for all time ${t}$,

\begin{equation}
p({y}_t | {y}_{<t}, {x}_{t}) = p({y}_t | {y}_{t-B:t-1}, {x}_{t}).
\tag2
\end{equation}

When this assumption is violated, $p({y}_t | {y}_{< t}, {x}_{t})$ has a different dependency structure at each ${t}$, so it changes by definition. Figure 2 illustrates this assumption compared to Figure 1.

It is worth noting that some widely-studied non-stationary stochastic processes, such as random walks or, more generally, unit-root processes, fall into the class of joint non-stationarity, where ${x} = \emptyset$ and the conditional distribution $p({y}_t | y_{< t})$ stays the same.

Existing Solutions

Assumption 1 separates two types of time series model families: those for which Assumption 1 is true and those for which it is not.

The latter class includes popular architectures like State-Space Models (SSMs) [1] and different incarnations of Recurrent Neural Networks (RNNs), such as those with Long Short-Term Memory (LSTM) [2] or Gated Recurrent Unit (GRU) [3]. In theory, these models do have the capability to model conditional non-stationarity, within the limits of their own recursive structural assumptions on the latent state, but they do not have any explicit inductive bias built into the model to account for non-stationarity. In practice, this means they still tend to suffer from non-stationarity, which can be present in either the training or test data.

In the class of models that satisfy Assumption 1 we have, among others, Autoregressive (AR) models [4], Temporal Convolutional Networks (TCNs) [5, 6], and more recently, Transformer variants [7, 8, 9] and N- BEATS [10]. Along with Assumption 1 they usually also assume conditional stationarity as part of their inductive bias. With stronger stationarity assumptions, they tend to perform well on data that satisfy these assumptions, but if non-stationarity, especially conditional non-stationarity, is present in either the training or test data, it can cause significant issues for the model to learn robustly and predict accurately. Specifically, if the training data have conditional non-stationarity, the data would seem to have inconsistent input-output relationships, and the model would not be able to learn “the” correct relationship. If the conditional distribution in the test data is different from the training data, the model would learn a “wrong” relationship that does not apply to the test data.

Adjacent Research Areas

A number of research areas are tightly related to the challenge of non-stationarity in time series modeling. We outline some of them in the following paragraphs but note that existing methods in these areas, although related, usually cannot be applied directly to time series.

Covariate non-stationarity as defined above is similar to covariate shift in domain adaptation and transfer learning [11, 12], although in the latter, the data are usually not time series, so there is no dependency of the target variable on itself (from previous time steps). In a typical scenario, a reasonable amount of labeled training data sampled from a distribution (source domain) are available, but the test data are assumed to be from a different distribution (target domain), wherein some invariance, such as the conditional distribution of the output given the input, is preserved. The goal is to adapt the model trained from the source-domain data such that it works well on the target-domain data.

Continual learning [13, 14] is another adjacent area, where the model needs to learn and adapt to multiple tasks (input-output relationships) online. Usually the data for each task arrive sequentially, and the model needs to not only keep learning new tasks but also avoid forgetting older ones [15]. An interesting special case is Bayesian continual learning [16, 17], which combines continual learning with Bayesian deep learning. The difference from typical continual learning is that a prior distribution is defined over the parameters of a deep neural network, and the posterior distribution over the parameters is inferred continually after observing new samples.

Dynamic Adaptation to Distribution Shifts @ Borealis AI

For time series modeling and forecasting in capital markets, we believe that conditional non-stationarity is the most common and important type of non-stationarity. We take a different approach to dealing with conditional non-stationary in time series than existing models like RNNs. The core of our architecture is the clean decoupling of the time-variant (non-stationary) part and the time-invariant (stationary) part of the signal. The time-invariant part models a stationary conditional distribution, given some control variables, while the time-variant part focuses on modeling the changes in this conditional distribution over time through those control variables. Using this separation, we build a flexible time-invariant conditional model and make efficient inferences about how the model changes over time. At test time, our model takes both the uncertainty of the conditional distribution and the non-stationarity into account when making predictions and adapts to the changes in the conditional distribution over time in an online manner.

Figure 3 shows a high-level illustration of the model. At the center of the model is the conditional distribution at each time step $t$, which we assume to be parameterized by the output of a (non-linear) function $f_t({y}_{t-B:t-1}) = f(g({y}_{t-B:t-1}); \chi_t)$ that conditions on the past $B$ observations, modulated by the non-stationary control variable $\chi_t$ (here we omit ${x}_t$ for simplicity). The past observations are summarized into a fixed-length vector through a time-invariant encoder $g$, such as a multilayer perceptron (MLP). The control variable $\chi_t$ changes over time through a dynamic model whose parameters are learned from the data along with the parameters of $g$. To train the model, we use variational inference and maximize the evidence lower bound (ELBO), where the variational model can be a very flexible generative model, such as an inverse autoregressive flow (IAF) [24]. At test time, however, we use Rao-Blackwellized particle filters [25] to keep inferring the posterior of $\chi_t$ at each time step $t$, after observing ${y}_t$, and use Monte-Carlo sampling to make predictions of ${y}_{t+1:t+H}$.

Non-Stationarity in Other Projects @ Borealis AI

Borealis AI supports a broad spectrum of domains within RBC, and many of the principles above generalize to applications outside capital markets, e.g., Personal and Commercial Banking (P&CB). While there is no shared environment or direct competition, in this case, the complex nature of human behaviours, which changes over time due to internal evolution and/or external influence, makes flexible adaptions to (asynchronous) time series data generated by client (trans)actions equally relevant. Many of the solutions we develop in the Photon team generalize to these new application domains with small modifications.

You can read the full paper ‘DynaConF: Dynamic Forecasting of Non-Stationary
Time-Series’ by Siqi Liu and Andreas Lehrmann at arXiv – 2209.08411 page.

References

[1] R E Kalman.A new approach to linear filtering and prediction problems. Transactions of the ASME-Journal of Basic Engineering, 82(Series D):35–45, 1960. ISSN 00219223. doi: 10.1115/1.3662552.

[2]  Sepp Hochreiter and Jürgen Schmidhuber. Long short-term memory. Neural computation, 9(8):1735– 1780, 1997.

[3]  Kyunghyun Cho, Bart van Merrienboer, Caglar Gulcehre, Dzmitry Bahdanau, Fethi Bougares, Holger Schwenk, and Yoshua Bengio. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. arXiv:1406.1078 [cs, stat], June 2014.

[4]  George EP Box, Gwilym M. Jenkins, Gregory C. Reinsel, and Greta M. Ljung. Time Series Analysis: Forecasting and Control. John Wiley & Sons, 2015.

[5]  Shaojie Bai, J. Zico Kolter, and Vladlen Koltun. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv preprint arXiv:1803.01271, 2018.

[6]  Colin Lea, Michael D. Flynn, Rene Vidal, Austin Reiter, and Gregory D. Hager. Temporal convolutional networks for action segmentation and detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 156–165, 2017.

[7]  Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is All you Need. Advances in Neural Information Processing Systems, 30, 2017.

[8]  Binh Tang and David S Matteson. Probabilistic Transformer For Time Series Analysis. In Advances in Neural Information Processing Systems, volume 34, pages 23592–23608. Curran Associates, Inc., 2021.

[9]  Haixu Wu, Jiehui Xu, Jianmin Wang, and Mingsheng Long. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting. In Advances in Neural Information Processing Systems, volume 34, pages 22419–22430. Curran Associates, Inc., 2021.

[10]  Boris N. Oreshkin, Dmitri Carpov, Nicolas Chapados, and Yoshua Bengio. N-BEATS: Neural basis expansion analysis for interpretable time series forecasting. arXiv:1905.10437 [cs, stat], February 2020.

[11]  Sinno Jialin Pan and Qiang Yang. A survey on transfer learning. Knowledge and Data Engineering, IEEE Transactions on, 22(10):1345–1359, 2010.

[12]  Mei Wang and Weihong Deng. Deep visual domain adaptation: A survey. Neurocomputing, 312:135–153, 2018.

[13]  Matthias De Lange, Rahaf Aljundi, Marc Masana, Sarah Parisot, Xu Jia, Ales Leonardis, Gregory Slabaugh, and Tinne Tuytelaars. A continual learning survey: Defying forgetting in classification tasks. IEEE Transactions on Pattern Analysis and Machine Intelligence, pages 1–1, 2021. ISSN 0162-8828, 2160- 9292, 1939-3539. doi: 10.1109/TPAMI.2021.3057446.

[14]  German I. Parisi, Ronald Kemker, Jose L. Part, Christopher Kanan, and Stefan Wermter. Continual life-long learning with neural networks: A review. Neural Networks, 113:54–71, May 2019. ISSN 0893-6080. doi: 10.1016/j.neunet.2019.01.012.

[15] James Kirkpatrick, Razvan Pascanu, Neil Rabinowitz, Joel Veness, Guillaume Desjardins, Andrei A.Rusu, Kieran Milan, John Quan, Tiago Ramalho, Agnieszka Grabska-Barwinska, Demis Hassabis, Claudia Clopath, Dharshan Kumaran, and Raia Hadsell. Overcoming catastrophic forgetting in neural networks. arXiv:1612.00796 [cs, stat], January 2017.

[16]  Cuong V. Nguyen, Yingzhen Li, Thang D. Bui, and Richard E. Turner. Variational Continual Learning. In International Conference on Learning Representations, February 2018.

[17]  Richard Kurle, Botond Cseke, Alexej Klushyn, Patrick van der Smagt, and Stephan Günnemann. Continual Learning with Bayesian Neural Networks for Non-Stationary Data. In International Conference on Learning Representations, September 2019.

[18]  Timothy M Hospedales, Antreas Antoniou, Paul Micaelli, and Amos J. Storkey. Meta-Learning in Neural Networks: A Survey. IEEE Transactions on Pattern Analysis and Machine Intelligence, pages 1–1, 2021. ISSN 1939-3539. doi: 10.1109/TPAMI.2021.3079209.

[19]  Sepp Hochreiter, A. Steven Younger, and Peter R. Conwell. Learning to learn using gradient descent. In International Conference on Artificial Neural Networks, pages 87–94. Springer, 2001.

[20]  Adam Santoro, Sergey Bartunov, Matthew Botvinick, Daan Wierstra, and Timothy Lillicrap. Meta-Learning with Memory-Augmented Neural Networks. In Proceedings of The 33rd International Conference on Machine Learning, pages 1842–1850. PMLR, June 2016.

[21]  Chelsea Finn, Pieter Abbeel, and Sergey Levine. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. In Proceedings of the 34th International Conference on Machine Learning, pages 1126–1135. PMLR, July 2017.

[22]  Chelsea Finn, Aravind Rajeswaran, Sham Kakade, and Sergey Levine. Online Meta-Learning. In Proceedings of the 36th International Conference on Machine Learning, pages 1920–1930. PMLR, May 2019.

[23]  Marvin Zhang, Henrik Marklund, Nikita Dhawan, Abhishek Gupta, Sergey Levine, and Chelsea Finn. Adaptive risk minimization: Learning to adapt to domain shift. Advances in Neural Information Processing Systems, 34:23664–23678, 2021.

[24] Diederik P. Kingma, Tim Salimans, Rafal Jozefowicz, Xi Chen, Ilya Sutskever, and Max Welling. Improving Variational Inference with Inverse Autoregressive Flow. arXiv:1606.04934 [cs, stat], January 2017.

[25] Arnaud Doucet, Nando de Freitas, Kevin Murphy, and Stuart Russell. Rao-Blackwellised Particle Filtering for Dynamic Bayesian Networks. arXiv:1301.3853, January 2013.