
Introduction
XLNet is the latest and greatest model to emerge from the booming field of Natural Language Processing (NLP). The XLNet paper combines recent advances in NLP with innovative choices in how the language modelling problem is approached. When trained on a very large NLP corpus, the model achieves state-of-the-art performance for the standard NLP tasks that comprise the GLUE benchmark.
XLNet is an auto-regressive language model which outputs the joint probability of a sequence of tokens based on the transformer architecture with recurrence. Its training objective calculates the probability of a word token conditioned on all permutations of word tokens in a sentence, as opposed to just those to the left or just those to the right of the target token.
If the above description made perfect sense, then this post is not for you. If it didn’t, then read on to find out how XLNet works, and why it is the new standard for many NLP tasks.
Language modelling
In language modelling we calculate the joint probability distribution for sequences of tokens (words), and this is often achieved by factorizing the joint distribution into conditional distributions of one token given other tokens in the sequence. For example, given the sequence of tokens New, York, is, a, city the language model could be asked to calculate the probability $Pr$(New | is, a, city). This is the probability that the token New is in the sequence given that is, a, and city are also in the sequence (figure 1).
For the purpose of this discussion, consider that generally a language model takes a text sequence of $T$ tokens, $\mathbf{x} = [x_1, x_2,\ldots, x_T]$, and computes the probability of some tokens $\mathbf{x}^{\prime}$ being present in the sequence, given some others $\mathbf{x}^{\prime\prime}$ in the sequence: $Pr(\mathbf{x}^{\prime} | \mathbf{x}^{\prime\prime})$ where $\mathbf{x}^{\prime}$ and $\mathbf{x}^{\prime\prime}$ are non-overlapping subsets of $\mathbf{x}$.
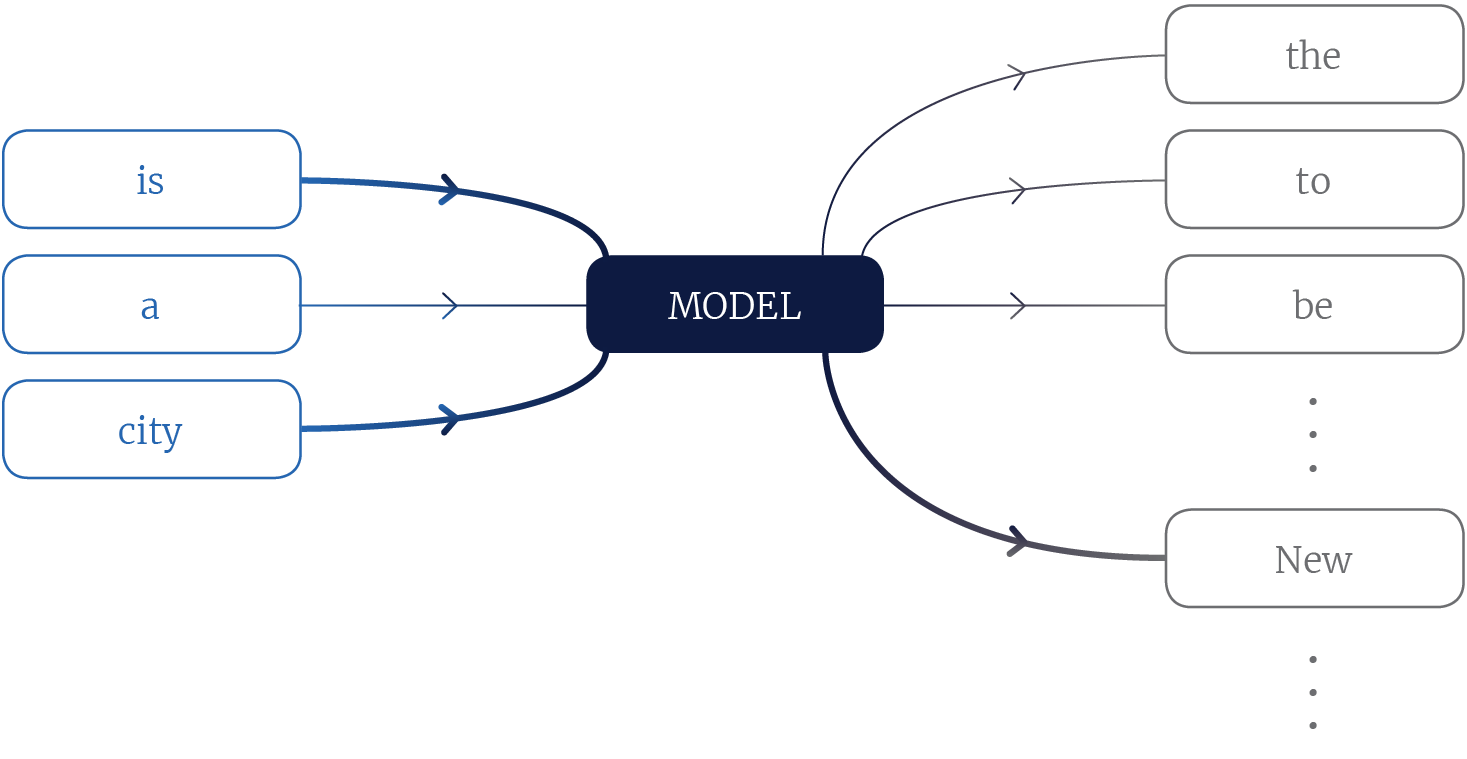
Figure 1, A language model. The model is a function which takes as input some context tokens and outputs a probability for each token in a vocabulary. Thicker lines indicate context words which are more informative and vocabulary words which are more likely.
Why would anyone want a model which can calculate the probability that a word is in a sequence? Actually, no-one really cares about that1. However, a model that contains enough information to predict what comes next in a sentence can be applied to other more useful tasks; for example, it might be used to determine who is mentioned in the text, what action is being taken, or if the text has a positive or negative sentiment. Hence, models are pre-trained with the language modeling objective and subsequently fine-tuned to solve more practical tasks.
Standing on the shoulders of giant models
Let’s discuss the architectural foundation of XLNet. The first component of a language model is a word-embedding matrix: a fixed-length vector is assigned for each token in the vocabulary and so the sequence is converted to a set of vectors.
Next we need to relate the embedded tokens in a sequence. A long-time favorite for this task has been the LSTM architecture which relates adjacent tokens (e.g. the ELMo model), but recent state of the art results have been achieved with transformers (e.g. the BERT model2). The transformer architecture allows non-adjacent tokens in the sequence to be combined to generate higher-level information using an attention mechanism. This helps the model learn from the long-distance relations that exist in text more easily than LSTM based approaches.
Transformers have a drawback: they operate on fixed-length sequences. What if knowing that New should occur in the sentence ____ York is a city also requires that the model have read something about the Empire State building in a previous sentence? Transformer-XL resolves this issue by allowing the current sequence to see information from the previous sequences. It is this architecture that XLNet is based on.
XL training objective
XLNet’s main contribution is not the architecture3, but a modified language model training objective which learns conditional distributions for all permutations of tokens in a sequence. Before diving into the details of that objective, let’s revisit the BERT model to motivate XLNet’s choices.
The previous state of the art (BERT) used a training objective that was tasked with recovering words in a sentence which have been masked. For a given sentence, some tokens are replaced with a generic [mask] token, and the model is asked to recover the originals.

Figure 2, Depiction of the BERT model. The model inputs are context tokens, some which are masked. By attending to the correct context tokens, the model can know that boat is a likely value for the masked token.
The XLNet paper argues that this isn’t a great way to train the model. Let’s leave the details of this argument to the paper and instead present a less precise argument that captures some of the important concepts.
A language model should encode as much information and nuances from text as possible. The BERT model tries to recover the masked words in the sentence The [mask] was beached on the riverside (figure 2). Words such as boat or canoe are likely here. BERT can know this because a boat can be beached, and is often found on a riverside. But BERT doesn’t necessarily need to learn that a boat can be beached, since it can still use riverside as a crutch to infer that boat is the masked token.
Moreover, BERT predicts the masked tokens independently, so it doesn’t learn how they influence one-another. If the example was The [mask] was [mask] on the riverside, then BERT might correclty assign high probabilities to (boat, beached) and (parade, seen) but might also think (parade, beached) is acceptable.
Approaches such as BERT and ELMo improved on the state of the art by incorporating both left and right contexts into predictions. XLNet took this a step further: the model’s contribution is to predict each word in a sequence using any combination of other words in that sequence. XLNet might be asked to calculate what word is likely to follow The. Lots of words are likely, but certainly boat is more likely than they, so it’s already learned something about a boat (mainly that it’s not a pronoun). Next it might be asked to calculate which is a likely 2nd word given [3]was, [4]beached. And, then it might be asked to calculate which is a likely 4th word given: [3]was, [5]on, [7]riverside.

Figure 3, Depiction of the XLNet model. It must calculate that boat is a likely token for many different contexts drawn from the sequence.
In this way XLNet doesn’t really have a crutch to lean on. It’s being presented difficult, and at times ambiguous contexts from which to infer whether or not a word is in a sentence. This is what allows it to squeeze more information out of the training corpus (figure 3).
In practice, XLNet samples from all possible permutations, so it doesn’t get to see every single relation. It also doesn’t use very small contexts as they are found to hinder training. After applying these practical heuristics, it bears more of a resemblance to BERT.
In the next few sections we’ll expand on the more challenging aspects of the paper.
Permutations
Given a sequence $\mathbf{x}$, an auto-regressive (AR) model is one which calculates the probability $Pr(x_i | x_{<i})$. In language modelling, this is the probability of a token $x_{i}$ in the sentence, conditioned on the tokens $x_{<i}$ preceding it. These conditioning words are referred to as the context. Such a model is asymmetric and isn’t learning from all token relations in the corpus.
Auto-regressive models such as ELMo allow a model to also learn from relations between a token and those following it. The AR objective in this case could be seen as $Pr(x_i) = Pr(x_i | x_{>i})$. It is auto-regressive in the reversed sequence. But why stop there? There could be interesting relations to learn from if we look at just the two nearest tokens: $Pr(x_i) = Pr(x_i | x_{i-1}, x_{i+1})$ or really any combination of tokens $Pr(x_i) = Pr(x_i | x_{i-1}, x_{i+2}, x_{i-3})$.
XLNet proposes to use an objective which is an expectation over all such permutations. Consider a sequence x = [This, is, a, sentence] with T=4 tokens. Now consider the set of all 4! permutations $\mathcal{Z}$ = {[1, 2, 3, 4], [1, 2, 4, 3],. . ., [4, 3, 2, 1]}. The XLNet model is auto-regressive over all such permutations; it can calculate the probability of token $x_i$ given preceding tokens $x_{<i}$ from any order $\mathbf{z}$ from $\mathcal{Z}$.
For example, it can calculate the probability of the 3rd element given the two preceding ones from any permutation. The three permutations [1, 2, 3, 4], [1, 2, 4, 3] and [4, 3, 2, 1] above would correspond to $Pr$(a, | This, is), $Pr$(sentence | This, is) and $Pr$(is | sentence, a). Similarly, the probability of the second element given the first would be $Pr$(is | This), $Pr$(is | This) and $Pr$(a | sentence). Considering all four positions and all 4! permutations the model takes into consideration all possible dependencies.
These ideas are embodied in equation 3 from the paper:
\begin{equation*}\hat{\boldsymbol\theta} = \mathop{\rm argmax}_{\boldsymbol\theta}\left[\mathbb{E}_{\mathbf{z}\sim\mathcal{Z}}\left[\sum_{t=1}^{T} \log \left[Pr(x_{z[t]}|x_{z[<t]}) \right] \right]\right]\end{equation*}
This criterion finds model parameters $\boldsymbol\theta$ to maximize the probability of tokens $x_{z[t]}$ in a sequence of length $T$ given preceding tokens $x_{z[<t]}$, where $z[t]$ is the t$^{th}$ element of a permutation $\mathbf{z}$ of the token indices and $z[<t]$ are the previous elements in the permutation. The sum of log probabilities means that for any one permutation the model is properly auto-regressive as it is the product of the probability for each element in the sequence. The expectation over all the permutations in $\mathcal{Z}$ shows the model is trained to be equally capable of computing probabilities for any token given any context.
Attention mask
There is something missing from the way the model has been presented so far: how does the model know about word order? The model can compute $Pr$(This | is) as well as $Pr$(This | a). Ideally it should know something about the relative position of This and is and also of a. Otherwise it would just think all tokens in the sequence are equally likely to be next to one-another. What we want is a model which predicts $Pr$(This | is, 2) and $Pr$(This | a, 3). In other words, it should know the indices of the context tokens.
The transformer architecture addresses this problem by adding positional information to token embeddings. You can think of the training objective terms as $Pr$(This | is+2). But if we really shuffled the sentence tokens, this mechanism would break. This problem is resolved by using an attention mask. When the model computes the context which is the input to the probability calculation, it always does so using the same token order, and simply masks those not in the context under consideration (i.e. those that come subsequently in the shuffled order).
As a concrete example, consider the permutation [3, 2, 4, 1]. When calculating the probability of the 1st element in that order (i.e., token 3), the model has no context as the other tokens have not yet been seen. So the mask would be [0, 0, 0, 0]. For the 2nd element (token 2), the mask is [0, 0, 1, 0] as its only context is token 3. Following that logic, the 3rdand 4th elements (tokens 4 and 1) have masks [0, 1, 1, 0] and [0, 1, 1, 1]. Stacking all those in the token order gives the matrix (as seen in fig. 2(c) in the paper):
\begin{equation}\begin{bmatrix}0& 1& 1& 1 \\0& 0& 1& 0\\0& 0& 0& 0 \\0& 1& 1& 0\end{bmatrix}\label{eqn:matrix-mask}\end{equation}
Another way to look at this is that the training objective will contain the following terms where underscores represent what has been masked:
$Pr$(This | ___, is+2, a+3, sentence+4)
$Pr$(is | ___, ___, a+3, ___)
$Pr$(a | ___, ___, ___, ___)
$Pr$(sentence | ___, is+2, a+3, ___)
Two-stream self-attention
There remains one oversight to address: we not only want the probability to be conditioned on the context token indices, but also the index of the token whose probability is being calculated. In other words we want $Pr$(This | 1, is+2): the probability of This given that it is the 1st token and that is is the 2nd token. But the transformer architecture encodes the positional information 1 and 2 within the embedding for This and is. So this would look like $Pr$(This | This+1, is+2). Unfortunately, the model now trivially knows that This is part of the sentence and should be likely.
The solution to this problem is a two-stream self-attention mechanism. Each token position $i$, has two associated vectors at each self-attention layer $m$: $\mathbf{h}_i^m$ and $\mathbf{g}_i^m$. The $\mathbf{h}$ vectors belong to the content stream, while the $\mathbf{g}$ vectors belong to the query stream. The content stream vectors are initialized with token embeddings added to positional embeddings. The query stream vectors are initialized with a generic embedding vector $\mathbf{w}$ added to positional embeddings. Note that $\mathbf{w}$ is the same no matter the token, and thus cannot be used to distinguish between tokens.
At each layer, each content vector, $\mathbf{h}_i$, is updated using those $\mathbf{h}$’s that remain unmasked and itself (equivalent to unmasking the diagonal from the matrix shown in the previous section). Thus, $\mathbf{h}_3$ is updated with the mask $[0, 0, 1, 0]$, while $\mathbf{h}_2$ is updated with the mask $[0, 1, 1, 0]$. The update uses the content vectors as the query, key and value.
By contrast, at each layer each query vector $\mathbf{g}_{i}$ is updated using the unmasked content vectors and itself. The update uses $\mathbf{g}_i$ as the query while it uses $\mathbf{h}_j$’s as the keys and values, where $j$ is the index of an unmasked token in the context of $i$.
Figure 4 illustrates how the the query $\mathbf{g}_4^m$ for the 4th token at the $m$th layer of self-attention is calculated. It shows that $\mathbf{g}_4^m$ is an aggregation of is+2, a+3 and the position 4, which is precisely the context needed to calculate the probability of the token sentence.

Figure 4, Dual attention mechanism for computation of $\mathbf{g}_{4}^{m}$, the $4^{\mbox{th}}$ token at the $m^{\mbox{th}}$ layer of self-attention. Arrows indicate the flow of information from vectors. Where lines intersect at a circle, self-attention query/key/value operations are performed and aggregated. The yellow lines represent the updates in the content stream for the third symbol (depends only itself) and second symbol (depends on itself and third symbol). The light blue lines represent the update in the query stream (depends on itself and the second and third symbols from the content stream).
To follow-along from the last section, the training objective contains the following terms where $*$ denotes that this is the token position whose probability is being computed:
$Pr$(This | *, is+2, a+3, sentence+4)
$Pr$(is | ___, *, a+3, ___)
$Pr$(a | ___, ___, *, ___)
$Pr$(sentence | ___, is+2, a+3, *).
Results
Does it work? The short answer is yes. The long answer is also yes. Perhaps this is not surprising: XLNet builds on previous state of the art methods. It was trained on a corpus of 30 billion words (an order of magnitude greater than that used to train BERT and drawn from more diverse sources) and this training required significantly more hours of compute time than previous models:
| ULMFit | 1 GPU day |
| ELMo | 40 GPU days |
| BERT | 450 GPU days |
| XLNet | 2000 GPU days |
Table 1. Approximate computation time for training recent NLP models4.
Perhaps more interestingly, XLNet’s ablation study shows that it also works better than BERT in a fair comparison (figure 5). That is, when the model is trained on the same corpus as was BERT, using the same hyperparameters and the same number of layers, it consistently outperforms BERT. Even more interestingly, XLNet also beats Transformer-XL in the fair comparison. Transformer-XL could be considered as an ablation of the permutation AR objective. The consistent improvement over that score is evidence for the strength of that method.
Ablation Results

Figure 5, Ablation study for XLNet for four the following four of the tested benchmarks: RACE, SQuAD2.0 F1, MNLI mm and SST-2. Results relative to BERT for matched training data. The different bars represent different training settings. They are described in section 3.7 of the paper.
What is not resolved by the ablation study is the contribution of the two-stream self-attention mechanism to XLNet’s performance gains. It both allows the attention mechanism to explicitly take the target token position into account, and it introduces additional latent capacity in the form of the query stream vectors. While it is an intricate part of the XLNet architecture, it is possible that models such as BERT could also benefit from this mechanism without using the same training objective as XLNet.
1 While the main purpose of pre-trained language models is to learn linguistic features which are useful in downstream tasks, the actual language model’s calculation of word probabilities can be useful for things like outlier detection and auto-correct.
2 The BERT model is technically a masked language model as it isn’t trained to maximize the joint probability of a sequence of tokens.
3 In order to implement the NADE-like training objective, the XLNet paper also introduces some novel architecture choices which are discussed in later sections. However, for the purpose of this post, it is convenient to first discuss XLNet’s goal to create a model which learns from bi-directional context, and then introduce the architectural work needed to achieve this goal.
4 These values were derived using a speculative TPU to GPU hour conversion as explained in this post and rounded semi-arbitrarily.